数学教学中培养学生创新能力的探索
内容提要:
本文从“通过一题多解,培养学生的创新能力;善于引导学生归纳和发现,培养学生的创新能力;善于联想和比较,培养学生在联想和比较中创新;通过一题的灵活多变,不断培养学生的创新素质”四个方面,阐述了在小学数学教学中,如何注重开发学生的潜能,培养学生的创新能力。
关键词:一题多解 引导归纳 联想比较 一题多变
素质教育要求我们充分尊重学生的主体性,注重开发学生的潜能,对于数学这门学科来说,其中创新能力是素质教育的核心,关键是培养学生的创造性思维能力,培养学生的创造性思维能力,这是培养新世纪新型建设人才的时代要求,也是教学的重任。我长期从事小学数学的教学工作,在教学的实践中,我从以下几方面抓了学生创新能力的培养。
一、通过一题多解,培养学生的创新能力;
在教学中,通过多角度思考,获得多种解题途径,可拓宽学生的思路,使学生感受到数学的奥秘和情趣,培养学生的创新意识。
例1、 某水泥厂去年生产水泥32400吨,今年前五个月的产量就等于去年全年的产量,照这样计算,这个水泥厂今年将比去年增产百分之几?(九年义务教育六年制小学数学第十二册)
解法一,预计今年的水泥产量为:32400÷5×12=77760,今年可比去年增产:(77760-32400)÷32400=140% 。
解法二,设去年的每月的水泥产量为“1”,则去年的水泥总产量为 12 ,今年前5个月的水泥产量即达12,今年全年的水泥产量应为:12/5 ×12 ,因此今年的水泥产量将比去年增加:(12/5 ×12-12)÷12=140%。或 12/5 ×12÷12-1=140% 。
解法三:同上,去年水泥总产量为 12 ,今年前5个月的水泥产量即达12,生产同去年同样多的水泥,今年可比去年少用7(12-5)个月,如这7个月继续生产,则可比去年多增加水泥产量7,因此可得,今年的水泥产量将比去年增加:7÷5=140%。
解法四:设今年每个月的水泥产量为“1”,则今年的水泥总产量为12,因为今年5个月的水泥产量就同去年相等,因此去年的水泥总产量则为5,因此可得,今年的水泥产量将比去年增加:(12-5)÷5=140%。
解法五:设去年的水泥总产量为“1”,则去年每月的水泥产量则为 1/12 ,今年每月的每月的水泥产量则为1/5 ,今年与去年每月的水泥产量比则为:1/5∶ 1/12 ,因为时间相同,因此可得,今年与去年的水泥总产量的比也为1/5 ∶1/12 ,因此可得,今年的水泥产量将比去年增加:( 1/5- 1/12 )÷ 1/12 =140%。
例如在学习了百分数应用题后,我出示了这样一题:“某校女生人数比男生人数少20%,问男生比女生多百分之几?”,并要求学生用不同的方法进行求解。学生在我的点拨和指导下,经过讨论,很快列出了不同的算式:(1)、因为男生人数为单位“1”,因此女生人数为:1-20%=80% ,因此男生比女生人数多:(1-80%)÷80% =25 % 。(2)、同上,女生人数是男生人数的:1-20%=80% ,又因为女生人数比男生人数少20% ,因此可得,男生比女生人多:20%÷80% =25 % 。(3)、同上,因为女生人数是男生人数的80%= 4/5 ,即女生人数与男生人数的比是4∶5,,因此可得,因此男生比女生人数多 :(5-4)÷4=25 % 。
通过一题多解不仅能拓宽学生的思维领域,增加学生的思维空间,同时通过总结,可揭示一些有规律性的东西,达到增长学生智能的目的。
二、善于引导学生归纳和发现,培养学生的创新能力
在数学教学中,如能引导学生进行归纳和发现,也能培养和提高学生的创新能力。
如在教学完了平面图形的面积计算公式后,我要求学生归纳出一个能概括各个平面图形面积计算的公式,我让学生进行讨论,经过讨论,学生们归纳出,在小学阶段学过的面积公式都可以用梯形的面积计算公式来进行概括,因为梯形的面积计算公式是:(上底 +下底)×高÷2 。因为长方形、正方形、平行四边形的上底和下底相等,即可将这公式变成:底(长、边长)×高(宽、边长)×2÷2 = 底(长、边长)×高(宽、边长);又因为将圆面积公式是根据长方形的面积公式推导出来的,因此,梯形的面积公式对圆也同样适用;当梯形的上底是零时,即梯形成了一个三角形,这时梯形的面积公式成了:底×高÷2 。这即成了三角形的面积公式。这样,不仅使学生能熟练掌握已学过的平面图形的面积公式,同时,也培养和提高了学生的创新能力。
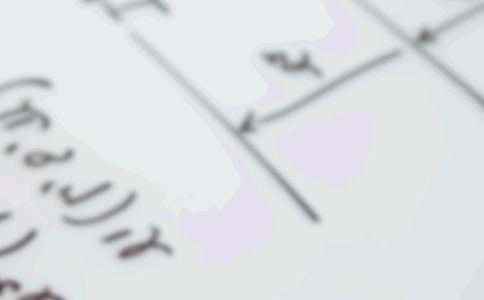
又如在教学了圆柱体的表面积公式后,学生掌握了圆柱体的表面积是侧面积加上两个底面积,我启发学生能否将圆面积的推导公式和圆柱体的侧面积推导公式的过程进行联想和联系,概括出求圆柱体表面积的公式。学生经过讨论并用学具操作,很快想出,因为将一个圆平均分成若干份,拼成一个近似长方形,这近似长方形的长即是圆柱体的底面周长,宽即是圆柱体的底面圆的半径,因此,圆柱体的表面积公式即可为:S=2πΥ×(Υ+H)。
三、善于联想和比较,培养学生在联想和比较中创新
在教学实践中,如让学生能针对某一问题,通过类比思维去解决,不仅能提高教学效果,还能培养学生的创新思维能力。
例如在教学了比的知识后,我出示了这样一句数量关系句:“某工厂男工人的人数比女工人的人数多 1/4 ” ,我要求学生根据这一句数量关系句进行联想,改变成内容不变但叙述方法不同的数量关系句,学生经过讨论,即很快能说出:(1)、男工人的人数是女工人的人数的1+1/4 = 5/4 ; (2)、某工厂男工人的人数与女工人的人数的比是5∶4 ;(3)、某工厂女工人的人数与男工人的人数的比是4∶5 ;(4)、某工厂女工人的人数是男工人的人数的 4/5 ,(5)、某工厂男工人的人数占全厂工人的人数的 5/9 ;(6)、某工厂女工人的人数占全厂工人的人数的4/9 ;(7)、某工厂女工人的人数比男工人的人数少 1/5 。这样学生很快能将比与分数进行融会贯通,增强了学生的创新意识。
又如在教学了数的整除的知识后,我出示了这样一题:“一个数被6除余4,被8除余2,被9除余1,这个最小是几?” 应该说这道题是有一定的难度的,学生求解会感到无从下手,这时,我出示了这样一题比较题:“一个数被6除余10,被8除余10,被9除余10,这个数最小是几?”这道题学生很快能求出答案:这个数即是6、8和9的最小公倍数多10,6、8和9的最小公倍数为72,因此这个数为:72+10=82;然后我引导学生将上道题与这道比较题进行想象和比较,学生很快知道,上道题只要假设被6除少商1余数即为10,被8除少商1余数也为10、被9除时少商1余数也为10,因此可迅速求得这个数只有减去10,就同时能被6、8和9整除,而6、8和9的最小公倍数为72,因此这个数为:72+10=82 。这样通过让学生展开联想和比较,不但可以提高学生的想象能力,也能提高学生的创新思维能力。
四、通过一题的灵活多变,不断培养学生的创新素质
在教学中,如果能做到引导学生对命题条件、结论进行各种变换,能充分调动学生学习的积极性。
例如在学习了长方体的表面积后,我让学生归纳出了求长方体的表面积公式后,我出示长方体的实物,并演示提出如果少掉一个底面的一个面,请学生思考这时五个面的面积公式又是怎样的?如果少掉前面的一个面,这时五个面的面积公式又是怎样的?如果少掉两个底面,这时的四个面的面积公式又是怎样的?少掉了两个底面,这时实际只要求什么?那一种物体只要求出四个面?学生经过讨论,很快能说出求五个面的面积公式,并知道少掉两个底面,实际上只要求长方体的侧面积,通风管即只要求四个面。这样通过运用实物和教具,让学生在实践中通过联想,增强了学生的创新意识,培养了学生的创造性思维能力,同时也提高了学生的解题能力。
再如课本上九年义务教育六年制小学数学第十二册中的的一道思考题:“修一条公路,已修和未修长度的比是1∶3,再修300米后,已修和未修长度的比是1∶2。这条路长多少米?”
这道题有的学生求解会有一定的难度,我就先出示了这样一道题:“修一条公路,已修了全长的1/4 ,再修300米后,则已修了全长的1/3 ,这条路长多少米?” 。 这道题学生很快能列出算式:300÷(1/3 -1/4 )=3600(米)。
然后我再引导学生思考,上面一道思考题的条件是:“再修300米后,已修和未修长度的比是1∶2” ,这里隐藏着一个等量关系,如果抓住这个等量关系,就可列方程解答。设已修的长度为X米,那么未修的长度为3X米。
(X+300)∶ (3 X-300)=l∶2
解得 X=900
X+3X=900+900×3=3600(米)
答:这条路长3600米。
接着,我再引导学生,又因为公路的总米数是“不变量”,把条件“已修和未修长度的比是1∶ 3,再修300米后,已修和未修长度的比是1∶ 2”转化为:“已修长度是未修长度的 1/3 ,再修300米,已修长度是未修长度的 1/2 ” ,如把公路全长看作单位“1” ,所以可得,已修的长度就是总长度的:1/3 ÷(1 + 1/3 )= 1/4 ,再修300米后,已修的长度就是总长度的:1/2 ÷(1+1/2 )= 1/3 ,由此可知,300米就相当于公路全长的:(1/3 -1/4 ) ,所以可列式为:300÷( 1/3 - 1/4 )=3600(米)。答:这条路有3600米。
在学生掌握了这道思考题的解答方法后,我又出示了这样一题:“修一条公路,已修长度是未修长度的是 1/3 ,再修300米后,已修长度是未修长度的1/2 。这条路长多少米?” 。然后我组织学生讨论,学生在掌握了上道题的解题方法后,很快能求出公路的全长是:300÷[ 1/2 ÷(1+1/2 )-1/3 ÷(1+1/3 )]=3600(米)。
接着,我又出示了这样一题:“修一条公路,未修长度是已修长度的3倍 ,再修300米后,未修长度是已修长度的 2倍 。这条路长多少米?” 。我再组织学生讨论,学生在解答了上面二题的基础上,也能很快求出这条公路的长度是:300÷[ 1÷(1+2)-1÷(1+3)]=3600(米)。
在长期的教学实践中,我认识到,数学教师要在课堂教学中培养学生的创造力,教师首先应创设一种民主、宽松、和谐的教学环境和教学气氛。有意识的培养学生的创新意识;善于激发学生的创造动机;发展学生的创造思维;树立学生具有创造力的个性品质。同时教师还要注意自身的知识和能力储备。教师自己能够打破传统定势,提高自身的认知水平,才能更加灵活的去引导学生的发展。更好的促进学生的发展。实现教书育人的目的
作者情况简介:
蒋 仪:小学高级老师 工作单位:江苏省江阴市青阳镇旌阳小学
邮政编码:214401 联系电话:0510——6517727
【数学教学中培养学生创新能力的探索】相关文章:
浅谈数学教学中创新能力的培养08-18
史教学中培养学生创新思维能力的探索与思考08-17
历史教学中对学生创新能力的培养08-18
在教学中培养学生的创新能力08-17
浅谈小学数学教学中创新能力的培养08-17
寓创新能力的培养于教学中08-17
初中物理教学中培养学生的创新能力08-02