精选八年级数学教案汇总5篇
作为一位不辞辛劳的人民教师,很有必要精心设计一份教案,教案是教学活动的依据,有着重要的地位。来参考自己需要的教案吧!以下是小编整理的八年级数学教案5篇,仅供参考,大家一起来看看吧。
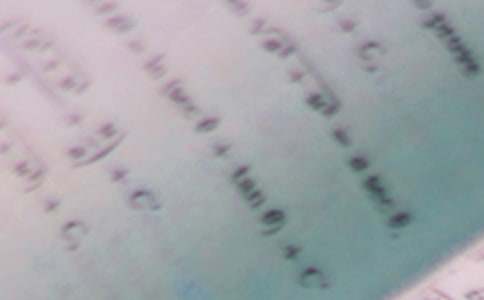
八年级数学教案 篇1
一、课堂引入
1.什么叫做平行四边形?什么叫做矩形?
2.矩形有哪些性质?
3.矩形与平行四边形有什么共同之处?有什么不同之处?
4.事例引入:小华想要做一个矩形像框送给妈妈做生日礼物,于是找来两根长度相等的短木条和两根长度相等的长木条制作,你有什么办法可以检测他做的是矩形像框吗?看看谁的方法可行?
通过讨论得到矩形的判定方法.
矩形判定方法1:对角钱相等的平行四边形是矩形.
矩形判定方法2:有三个角是直角的四边形是矩形.
(指出:判定一个四边形是矩形,知道三个角是直角,条件就够了.因为由四边形内角和可知,这时第四个角一定是直角.)
二、例习题分析
例1(补充)下列各句判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形;(×)
(2)有四个角是直角的四边形是矩形;(√)
(3)四个角都相等的四边形是矩形;(√)
(4)对角线相等的四边形是矩形;(×)
(5)对角线相等且互相垂直的四边形是矩形;(×)
(6)对角线互相平分且相等的四边形是矩形;(√)
(7)对角线相等,且有一个角是直角的四边形是矩形;(×)
(8)一组邻边垂直,一组对边平行且相等的四边形是矩形;(√)
(9)两组对边分别平行,且对角线相等的四边形是矩形.(√)
指出:
(l)所给四边形添加的.条件不满足三个的肯定不是矩形;
(2)所给四边形添加的条件是三个独立条件,但若与判定方法不同,则需要利用定义和判定方法证明或举反例,才能下结论.
例2(补充)已知ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4cm,求这个平行四边形的面积.
分析:首先根据△AOB是等边三角形及平行四边形对角线互相平分的性质判定出ABCD是矩形,再利用勾股定理计算边长,从而得到面积值.
解:∵ 四边形ABCD是平行四边形,
∴AO=AC,BO=BD.
∵ AO=BO,
∴ AC=BD.
∴ ABCD是矩形(对角线相等的平行四边形是矩形).
在Rt△ABC中,
∵ AB=4cm,AC=2AO=8cm,
∴BC=(cm).
例3(补充)已知:如图(1),ABCD的四个内角的平分线分别相交于点E,F,G,H.求证:四边形EFGH是矩形.
分析:要证四边形EFGH是矩形,由于此题目可分解出基本图形,如图(2),因此,可选用“三个角是直角的四边形是矩形”来证明
八年级数学教案 篇2
知识技能
1.了解两个图形成轴对称性的性质,了解轴对称图形的性质。
2.探究线段垂直平分线的性质。
过程方法
1.经历探索轴对称图形性质的过程,进一步体验轴对称的特点,发展空间观察。
2.探索线段垂直平分线的性质,培养学生认真探究、积极思考的能力。
情感态度价值观通过对轴对称图形性质的探索,促使学生对轴对称有了更进一步的认识,活动与探究的过程可以更大程度地激发学生学习的主动性和积极性,并使学生具有一些初步研究问题的能力。
教学重点
1.轴对称的性质。
2.线段垂直平分线的'性质。
教学难点体验轴对称的特征。
教学方法和手段多媒体教学
过程教学内容
引入中垂线概念
引出图形对称的性质第一张幻灯片
上节课我们共同探讨了轴对称图形,知道现实生活中由于有轴对称图形,而使得世界非常美丽。那么我们今天继续来研究轴对称的性质。
幻灯片二
1、图中的对称点有哪些?
2、点A和A的连线与直线MN有什么样的关系?
理由?:△ABC与△ABC关于直线MN对称,点A、B、C分别是点A、B、C的对称点,设AA交对称轴MN于点P,将△ABC和△ABC沿MN对折后,点A与A重合,于是有AP=AP,MPA=MPA=90。所以AA、BB和CC与MN除了垂直以外,MN还经过线段AA、BB和CC的中点。
我们把经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
定义:经过线段的中点并且垂直于这条线段,就叫这条线段的垂直平分线,也叫中垂线。
八年级数学教案 篇3
数据的波动
教学目标:
1、经历数据离散程度的探索过程
2、了解刻画数据离散程度的三个量度极差、标准差和方差,能借助计算器求出相应的数值。
教学重点:会计算某些数据的极差、标准差和方差。
教学难点:理解数据离散程度与三个差之间的关系。
教学准备:计算器,投影片等
教学过程:
一、创设情境
1、投影课本P138引例。
(通过对问题串的解决,使学生直观地估计从甲、乙两厂抽取的20只鸡腿的平均质量,同时让学生初步体会平均水平相近时,两者的离散程度未必相同,从而顺理成章地引入刻画数据离散程度的一个量度极差)
2、极差:是指一组数据中最大数据与最小数据的差,极差是用来刻画数据离散程度的一个统计量。
二、活动与探究
如果丙厂也参加了竞争,从该厂抽样调查了20只鸡腿,数据如图(投影课本159页图)
问题:1、丙厂这20只鸡腿质量的平均数和极差是多少?
2、如何刻画丙厂这20只鸡腿质量与其平均数的差距?分别求出甲、丙两厂的20只鸡腿质量与对应平均数的差距。
3、在甲、丙两厂中,你认为哪个厂鸡腿质量更符合要求?为什么?
(在上面的'情境中,学生很容易比较甲、乙两厂被抽取鸡腿质量的极差,即可得出结论。这里增加一个丙厂,其平均质量和极差与甲厂相同,此时导致学生思想认识上的矛盾,为引出另两个刻画数据离散程度的量度标准差和方差作铺垫。
三、讲解概念:
方差:各个数据与平均数之差的平方的平均数,记作s2
设有一组数据:x1, x2, x3,,xn,其平均数为
则s2= ,
而s= 称为该数据的标准差(既方差的算术平方根)
从上面计算公式可以看出:一组数据的极差,方差或标准差越小,这组数据就越稳定。
四、做一做
你能用计算器计算上述甲、丙两厂分别抽取的20只鸡腿质量的方差和标准差吗?你认为选哪个厂的鸡腿规格更好一些?说说你是怎样算的?
(通过对此问题的解决,使学生回顾了用计算器求平均数的步骤,并自由探索求方差的详细步骤)
五、巩固练习:课本第172页随堂练习
六、课堂小结:
1、怎样刻画一组数据的离散程度?
2、怎样求方差和标准差?
七、布置作业:习题5.5第1、2题。
八年级数学教案 篇4
教学目标
知识与技能
用二元一次方程组解决有趣场景中的数字问 题和行程问题,归纳用方程(组)解决实际问题的一般步骤.
过程与方法
1.通过设置问题串,让学生体会分析复杂问题的思考方法.
2.让学生进一步经历和体验列方程组解决实际问题的过程,体会方程组是刻画现实世界 的有效数学模型.
情感态度与价值观
在学习过程中让学生体验把复杂问题化为简单问题的策略,体验成功感,同时培养学生克服困难的意志和勇气, 树立自信心,并鼓励学生合作 交流,培养学生的团队精神.
教学重点
1.初步体会列方程组解决实际问题的步骤.
2.学会用图表 分析较复杂的数量关系问题。
教学难点
将实际问题转化 成二元一次方程组的数学模型;会用图表分析数 量关系。
教学准备:
教具:教材,课件,电脑(视频播放器)
学具:教材,练习本
教学过程
第一环节:复习提问(5分钟,学生口答)
内容:填空:
(1)一个两位数,个位数字是 ,十位数字是 ,则这个两位数用代数式表示为 ;若交换个位和十位上的数字得到一个新的两位数,用代数式表示为 .
(2)一个两位数,个位上的数为 ,十位上的数为 ,如果在它们之间添上一个0,就得到一个三位数,这个三位数用代数式可以表示为 .
(3)有两个两位数 和 ,如果将 放在 的左边,就得到一个四位数,那么这个四位数用代数式表示为 ;如果将 放在 的右边,将得到一个新的'四位数,那么这个四位数用代数式可表示为 .
第二环节:情境引入(10分钟,学生动脑思考,全班交流)
内容:小明爸爸骑着摩托车带着小明在公路上匀速行驶,下图是小明每隔1小时看到的里程情况.你能 确定小明在12:00时看到的里程碑上的数吗?
第三环节:合作学习(10分钟,小组讨论,找等量关系,解决 问题)
内容:例1
两个两位数的和是68,在较大的两位数的右边接着写较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数.已知前一个四位数比后一个四位数大2178,求这两个两位数.
学生先独立思考例1,在此基础上,教师根据学生思考情况组织交流与讨论.
第四环节:巩固练习(10分钟,学生尝试独立解决问题,全班交流)
内容:练习
1.一个两位数,减去它的各位数字之和的3倍,结果是23;这个两位数除以它的各位数字 之和,商是5,余数是1.这个两位数是多少?
2.一个两位数是另一个两位数的3倍,如果把这个两位数放在另一个两位数的左 边与放在右边所得的数之和为8484.求这个两位数.
第五环节:课堂小结(5分钟,教师引导学生总结一般步骤)
内容:
1.教师提问:本节课我们学习了那些内容,对这些内容你有什么体会和想法?请与同伴交流.
2.师生互相交流总结出列方程(组)解决实际问题的一般步骤.
第 六环节:布置作业
内容:习题7.6
A组(优等生) 2,3,4
B组(中等生)2、3
C组(后三分之一生)2
八年级数学教案 篇5
教学目标:
1、经历对图形进行观察、分析、欣赏和动手操作、画图过程,掌握有关画图的操作技能,发展初步审美能力,增强对图形欣赏的意识。
2、能按要求把所给出的图形补成以某直线为轴的轴对称图形,能依据图形的轴对称关系设计轴对称图形。
教学重点:本节课重点是掌握已知对称轴L和一个点,要画出点A关于L的轴对称点的画法,在此基础上掌握有关轴对称图形画图的操作技能,并能利用图形之间的轴对称关系来设计轴对称图形,掌握有关画图的技能及设计轴对称图形是本节课的难点。
教学方法:动手实践、讨论。
教学工具:课件
教学过程:
一、 先复习轴对称图形的定义,以及轴对称的相关的性质:
1.如果一个图形沿一条直线折叠后,直线两旁的部分能够互相________,那么这个图形叫做________________,这条直线叫做_____________
2.轴对称的三个重要性质______________________________________________
_____________________________________________________________________
二、提出问题:
二、探索练习:
1. 提出问题:
如图:给出了一个图案的一半,其中的虚线是这个图案的.对称轴。
你能画出这个图案的另一半吗?
吸引学生让学生有一种解决难点的想法。
2.分析问题:
分析图案:这个图案是由重要六个点构成的,要将这个图案的另一半画出来,根据轴对称的性质只要画出这个图案中六个点的对应点即可
问题转化成:已知对称轴和一个点A,要画出点A关于L的对应点 ,可采用如下方法:`
在学生掌握已知一个点画对应点的基础上,解决上述给出的问题,使学生有一条较明确的思路。
三、对所学内容进行巩固练习:
1. 如图,直线L是一个轴对称图形的对称轴,画出这个轴对称图形的另一半。
2. 试画出与线段AB关于直线L的线段
3.如图,已知 直线MN,画出以MN为对称轴 的轴对称图形
小 结: 本节课学习了已知对称轴L和一个点如何画出它的对应点,以及如何补全图形,并利用轴对称的性质知道如何设计轴对称图形。
教学后记:学生对这节课的内容掌握比较好,但对于利用轴对称的性质来设计图形觉得难度比较大。因本节课内容较有趣,许多学生上课积极性较高
【八年级数学教案】相关文章:
八年级的数学教案12-14
八年级数学教案06-18
八年级上册人教版数学教案02-27
八年级数学教案人教版01-03
八年级下册数学教案01-01
八年级的数学教案15篇12-14
八年级数学教案【荐】12-06
初中八年级数学教案11-03
人教版八年级数学教案11-04
【热门】八年级数学教案11-29